Un avión vuela horizontalmente a la altura H=4km sobre la superficie de la tierra a velocidad supersónica. El ruido llega al observador al cabo del tiempo t=10s de haber pasado el avión sobre él. Determinar la velocidad v del avión. La velocidad del sonido es c=330m/s.
Conocimiento previo
Como sabemos, el sonido es una onda mecánica tridimensional, cuyo medio de propagación es el aire. Cuando un objeto emite un sonido, éste se propaga a una velocidad de 340 m/s (en la solución trabajaremos con el valor dado en el enunciado). Los frentes de onda, que son algo así como el perfil de la onda, se propagan de manera esférica en el espacio. Cuando el emisor de sonido está en movimiento, respecto a un observado que se considera fijo, estos frentes de ondas se deforman un poco (ver imagen).
 |
| IMAGEN 1 Ondas esféricas ocasionadas por el disparo de una bala |
Si la velocidad de la fuente es menor que la velocidad del sonido, la fuente se mantendrá en el "interior" de estos frentes de onda. Por eso cuando viajamos en un automóvil, que por lo general va a velocidad mucho menor que la del sonido, podemos escuchar el motor. En cambio si la fuente de sonido se mueve a una velocidad igual a la velocidad del sonido, la fuente se mueve junto con el frente de onda. Una situación completamente diferente es cuando la fuente de sonido se mueve más rápido que la velocidad del sonido. En este caso la fuente sobre pasa al frente de onda y se encuentra, por tanto "fuera" del frente de onda que produce. Por ejemplo, los pilotos que vuelan aviones militares supersónicos no pueden escuchar el sonido del avión, porque van tan rápido que el propio sonido no tiene tiempo de llegar a ellos mismos. Estos tres casos se resumen en la siguiente imagen.
 |
| IMAGEN 2 En el caso 1, la fuente se mueve más lento que el sonido. En el caso 2 la fuente se mueve con igual velocidad del sonido. En el caso 3 la fuente ha sobrepasado la velocidad del sonido. |
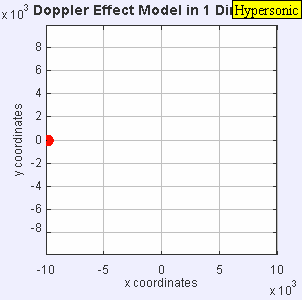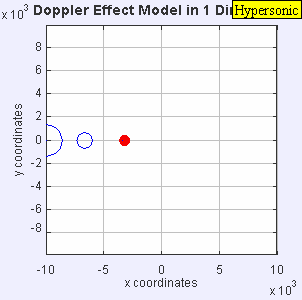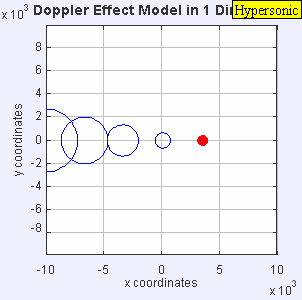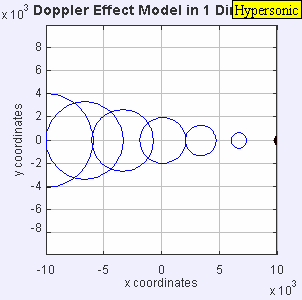 |
| IMAGEN 3 |
Como observamos la fuente es tan rápida que va dejando en el camino a cada frente de onda que produce.
Pues bien, necesitábamos este conocimiento previo para entender la situación que se expone en el problema y hacer nuestra solución al mismo.
Solución
 |
| IMAGEN 4 |
En la imagen 4 tenemos un esquema de la situación. Se señala el frente de onda circular que intersecta al observador en el punto B. En el punto C, que es el centro del frente de onda, el avión emitió el sonido. En el punto H el avión pasa sobre el observador. Y cuando el avión llega al punto A, después de 10 segundos de haber pasado por H, el sonido emitido en C llega al observador en B. Este esquema corresponde pues con el de un avión que se mueve a velocidad supersónica y como notamos en la figura 3 de la imagen 2.
Sea v la velocidad del avion que recorre la distancia HA en el tiempo t=10s, entonces
HA = vt . También según el problema la altura BH = h. Por tanto en la imagen 4 observando el triángulo BHA tenemos que, por el teorema de pitágoras: $$AB=\sqrt { { h }^{ 2 }+{ (vt) }^{ 2 } } \quad \quad \quad (1)$$ Luego también notamos que por semejanza de los triángulos BHA y ABC se cumple $$\cfrac { AC }{ BC } =\cfrac { AB }{ h } \quad \rightarrow \quad AC=\cfrac { AB\times BC }{ h } \quad \quad \quad (2)$$
El tiempo que el avión demora en ir del punto C al punto A, es decir la distancia AC es igual al tiempo que el sonido emitido en C demora en llegar al observador en B. Por tanto tenemos $$\cfrac { BC }{ c } =\cfrac { AC }{ v } \quad \quad \quad (3)$$ Reemplazando (2) en (3) $$\cfrac { BC }{ c } =\cfrac { AB\times BC }{ hv } \quad \rightarrow \quad AB=h\cfrac { v }{ c } \quad \quad \quad (4)$$ Igualando (1) y (4) $$\sqrt { { h }^{ 2 }+{ (vt) }^{ 2 } } =h\cfrac { v }{ c } \quad \rightarrow \quad v=\frac { h }{ \sqrt { \cfrac { { h }^{ 2 } }{ { c }^{ 2 } } -{ t }^{ 2 } } }$$
Por fin llegamos a una expresión para la velocidad del avión, ahora reemplazemos los datos dados por el problema $$\quad v=\frac { 4000m }{ \sqrt { \cfrac { { (4000m) }^{ 2 } }{ { (330m{ s }^{ -1 }) }^{ 2 } } -{ (10s) }^{ 2 } } }$$ $$\quad v\quad =\quad 584\quad m/s$$
Como era de esperarse la velocidad del avión es mayor que la del sonido. Sin duda un lindo problema donde aprendimos un poco sobre lo que sucede cuando un objeto se mueve más rápido que la velocidad del sonido. :)
PSDT: Les dejo este vídeo donde podemos ver a un caza militar rompiendo la barrera del sonido. Bye :)
No hay comentarios:
Publicar un comentario